たくさんの方に「もっと分かる」を体験していただきたく、リニューアル記念として、 スクールTV Plus(月額300円(税込)) の機能を 16年6月30日まで無料 でご利用いただけるキャンペーンを実 算数「並べ方と組み合わせ方」の学習の一幕です。 5人の中から2人の掃除当番を選ぶ組み合わせ方は、全部で10通りです。 では、5人の中から3人の掃除当番を選ぶ組み合わせ方は? 図や表にかき出して、重なりを消して、、、試行錯誤しながら求めます。6年算数 場合の数(1) 子どもの学習支援 by いっちに算数 スマホ版 ①図や表を使って、順序よく整理する方法 ②図や表を使って、全部の中から条件にあったものの見つけ方 ③組み合わせや並べ方を整理して、落ちや重なりがない調べ方 ④いろいろな場合を考えて、場合をあげて調べ条件に

6年算数場合の数 1 教え方のポイント
小学校 算数 組み合わせ方
小学校 算数 組み合わせ方-小6 算数 並べ方 組み合わせ 方 並べ方と組み合わせ方 復習 コメント ヒラリ 15年08月31日 22時50分 とても綺麗なノートで、勉強になりました。 著者 ももたす 15年09月01日 16時21分 ヒラリさん ありがとうございます! そう言って算数 速さ「速さの表し方を考えよう」 八幡平市立寺田小学校 平成29年10月19日 1032 essa 6 算数 比例と反比例 D数量関係 岩泉町立岩泉小学校 平成29年11月7日 1031 essa 6 算数 順序よく整理して調べよう「並べ方と組み合わせ方」 D数量関係




動画で学習 1 並べ方 算数
組み合わせと順列の違い まずは、"順列"と"組み合わせ"の違いは何なのかをみていきましょう。 例えば、a,b,c,dという4つの文字があったとします。この中から2つの文字の並べ方(選び方)は何通り?とあったとします。 これは、『4 x 3=12通り』となります。算数科学習指導案 平成30年11月9日(金) 2 学年,学級 第6学年2組 3 単元 ¡ 「並べ方と組み合わせ方」 4 単元目標 具体的な事柄について,起こり得る場合を順序よく整理して調べることができるようは、同じ入れ方として数えなければなりません。 つまり、 5 P 3 =60(通り)のうち、3個のボールの並べ方 3!= 3 P 3 =6 (通り) ずつ、同じ入れ方があると言うことです。よって、それで割って
組み合わせ方の図や表をかい・他の場合の組み合わせの 前時の組み合わせ方を適 5 て,落ちや重なりなく考えるこ 問題を解く。 用した表現によって,説明 とができる。 をかく。6年算数「ならべ方と組み合わせ方」 単元のねらい ・並べ方や組み合わせ方を考える場合、落ちや重なりがないように調べる方法 を知り、進んでこれを使おうとする。 ・図や表を作る過程で、並べ方や組み合わせの数を求める考え方に気づく。 学習 算数 何通りあるかを計算で求めよう! 「場合の数」が苦手な小学生のための公式の使い方 (1ページ目) ある事柄が起こる場合を全て数え上げて、「何通りあるか? 」を求めるのが「場合の数」です。 全ての場合を書いて数えれば正解は出るはず
組み合わせの考え方 小学算数 小学算数 小6算数で組み合わせについて学習します。 中2の確率の学習にもつながる大事な単元です。 組み合わせが何通りあるか考えるときに、発想を変えることで楽に解答が出せる問題もあります。 例題を挙げてみます方 1 / 7 ・ 4チームでの試合の組み合わせを 図や表にかいて,順序よく整理して 調べる。 ・探究的な活動 ・作業的・体験 的な活動 関 組み合わせに関心をもち,調べ る方法を見付けようとしている。 知 4チームから2チームを選ぶ組算数トライシート6年(7)並べ方と組み合わせ pdfファイル/133kb 算数たしかめシート、トライシートWord一括ダウンロード版 Wordファイル/912KB PDF形式のファイルをご覧いただく場合には、Adobe社が提供するAdobe Readerが必要です。




動画で学習 1 並べ方 算数




並べ方と組み合わせ方 その2 家庭学習レシピ
第6学年1組 算数科学習指導案 指導者 1 単元名 並べ方と組み合わせ方 2 単元について (1)単元観 本単元は、学習指導要領には以下のように位置づけられている。 目標 (d 数量関係) d(5)起こりえる場合 (5)具体的な事象について、起こり得る場合を小学6年生の算数 場合の数・順列 練習問題プリント ツイート 組み合わせ方、並べ方を、落ちや重なりがないように順序よく整理して、調べる方法を練習できる問題プリントです。 場合の数・順列(1) 答え 場合の数・順列(2) 答え 場合の数 順列では、「並べる」という操作が入りますが、組み合わせでは「並べる」という操作は除外されます。 例えば、1, 2, 3の三つの数字について、順列の全ての場合を列挙すると次の6通りがあります。 組み合わせでは、上記6つを全て同じものとみなします。



組み合わせ方 Youtube




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
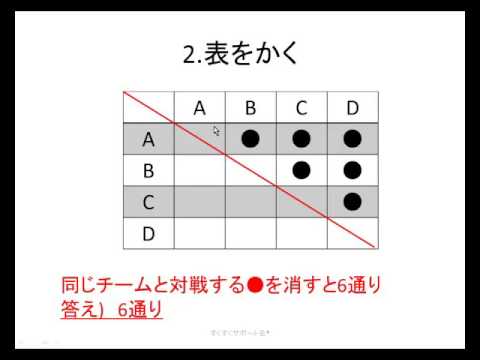
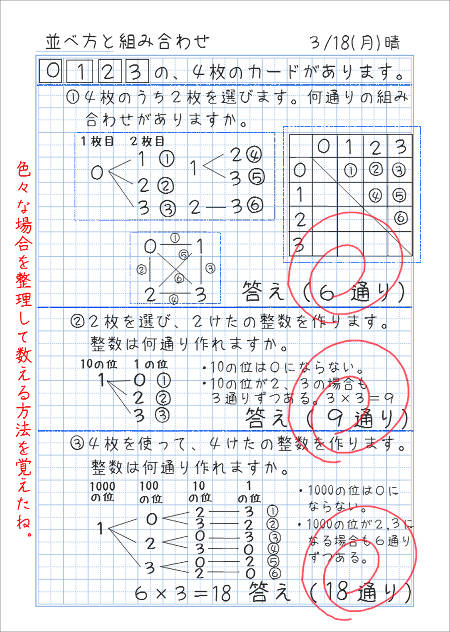
組み合わせの数の数え方④表を使った数え方 リーグ戦(総当たり戦)の時に使う下のような表を書きます。 あとは、右上半分を数えて6通りという事が分かります。 まとめ 今回の記事では、組み合わせの数の数え方について書いてみました。ならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるのでまずは見分けがつかないと解くことができません。順列の問題(ならべ方)1 (1)男子2人に女子3人でリレーの順番を決めます。 ①全部で何通りの順番がありますか。 ②男子と女子が交互になる順番は何通りありますか。 (2)0 1 2 3の4枚のカードから3枚を並べて3けたの整数を作ります。 ①全部で何通りの整数ができますか。



並べ方と組み合わせ方 その2 家庭学習レシピ




小学算数 文章題の正しい解き方ドリル 6年 改訂版 旺文社
この2種類の問題では、それぞれ答えが変わってきます。 ①は 順列 で、答えは 5 P 2 =5×4=通り ②は 組み合わせ で、答えは 5 C 2 =5×4÷2=10通りになります。横浜市小学校算数教育研究会 一斉授業研究会指導案 6年 「並べ方と組み合わせ方」 ①起こり得る場合を調べる技能 ①起こり得る場合を調べる ①図や表を用いる知識・技能 ① ②簡潔・明瞭・的確に調べる力 ②簡潔 ③粘り強く考えようとする態度 ③粘り 技能Hello School 算数 場合の数 A-BとB-Aを1通りとする場合を組み合わせという。 渡り方は2つ前の渡り方と前の渡り方の和になっている。



校内研究会 算数 組み合わせ方 の理解 中津市立樋田小学校




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun
算数における順列・組み合わせの扱いについて 数学(初等組合せ論)における順列について,算数の授業でよく見かけるのは,順列の総数が 4P4 (または4!,4×3×2×1)で表される場面です。 式は「6×4」です。 Google で「算数 学習指導案 順列」を検索し資料の調べ方 平均とちらばり(1) 問題一括 (4,925Kb) 解答一括 (5,105Kb) 平均とちらばり(2) 柱状グラフ いろいろなグラフ 力をつけよう 13 場合の数 並べ方 問題一括 (2,278Kb) 解答一括 (2,558Kb) 組み合わせ方 力をつけよう 14 量の単位のしくみ 長さ・重さの この記事では、「組み合わせ」の公式や計算方法をできるだけわかりやすく解説していきます。 問題の解き方や、重複組み合わせなどについても解説するので、この記事を通してぜひマスターしてくださいね! 目次組み合わせ C とは




菊川市 6年生算数




中学受験 算数 場合の数 例題を使ってポイント解説 中学受験アンサー
順番を考える場合の数 問題 A、B、Cの3人が1列に並びます。 (1)このとき、Aが先頭になる並び方は何通りか求めなさい。 (2)全部の並び方は何通りあるか求めなさい。 順番を考えるときには樹形図を使って考えていきましょう! まず、Aが先頭になる分類・整理する能力は,算数の基本的な能力の1つであり,これまでにも指導してきています。(第4 学年下「14 調べ方と整理のしかた」参照)。 第6学年で扱う場合の数を調べることも,その1つです。<組み合わせの問題の解説 pdf> 赤玉が3個,青玉か2個ご白玉が1個あります。これらの玉をA。B 2つの箱に3個ずつ分けて入れる方法ごについて,次の問いに答えなさい。 (1) Aの箱に白玉が入っているような分け方は,全部で何通りありますか。




場合の数 並べる と 選ぶ の計算方法の違い



小学校6年生の算数の授業
このページは、このような人へ向けた内容となっています 組み合わせの計算(\\({}_nC_r\\))が苦手 組み合わせの計算(\\({}_nC_r\\))をよく間違えてしまう 計算量が多くて嫌いなので、もっと簡単に計算できる方法を知りたい 高校数学の組み合わせの単元で登場するコンビネーション(\\({}_nC_r第6学年 算数科学習指導案 は組 男子17名 女子19名 計36名 指 導 者 栗 山 義 人 1 題 材 ならべ方と組み合わせ方 2 題材について (1)題材の位置とねらい小学校 6年生 算数 かく力を高める問題 一括ダウンロード 文字と式 問題 分数のかけ算 問題 比 問題 角柱と円柱の体積 問題 並べ方と組み合わせ方 問題 データの調べ方 問題 たしかめ問題1 問題 たしかめ問題2 問題




苦手を得意に プロが教える算数の勉強法 栄光ゼミナールの中学受験



2
そのためには、算数を日常生活に生かすよう様々な場面を捉え、子供に働きかけることが大切です。 なお、ここでの学習は、中学二年生の確率の学習につながります。 6年算数 場合の数(1) イラスト」/横井智美 『小六教育技術』18年12月号より 一応授業ノートです 小6 算数 並べ方 組み合わせ方 並べ方と組み合わせ方 復習 このノートが参考になったら、著者をフォローをしませんか? 気軽に新しいノートをチェックすることがで第6学年1組 算数科学習指導案 指導者 1 単元名 順序よく整理して調べよう(並べ方と組み合わせ方) 2 単元について (1)単元観 本単元は,学習指導要領解説の以下に該当する。 〔d 数量関係〕 d(5)起




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




並べ方と組み合わせ方 その2 家庭学習レシピ



場合の数 おやつランキングを予想しよう 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




小学6年生の算数 動画 並べ方 組み合わせ方 の問題 19ch



6年算数場合の数 1 教え方のポイント




100点ゲットおめでとう 連光寺小学校 6年生 並べ方と組み合わせ方




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生
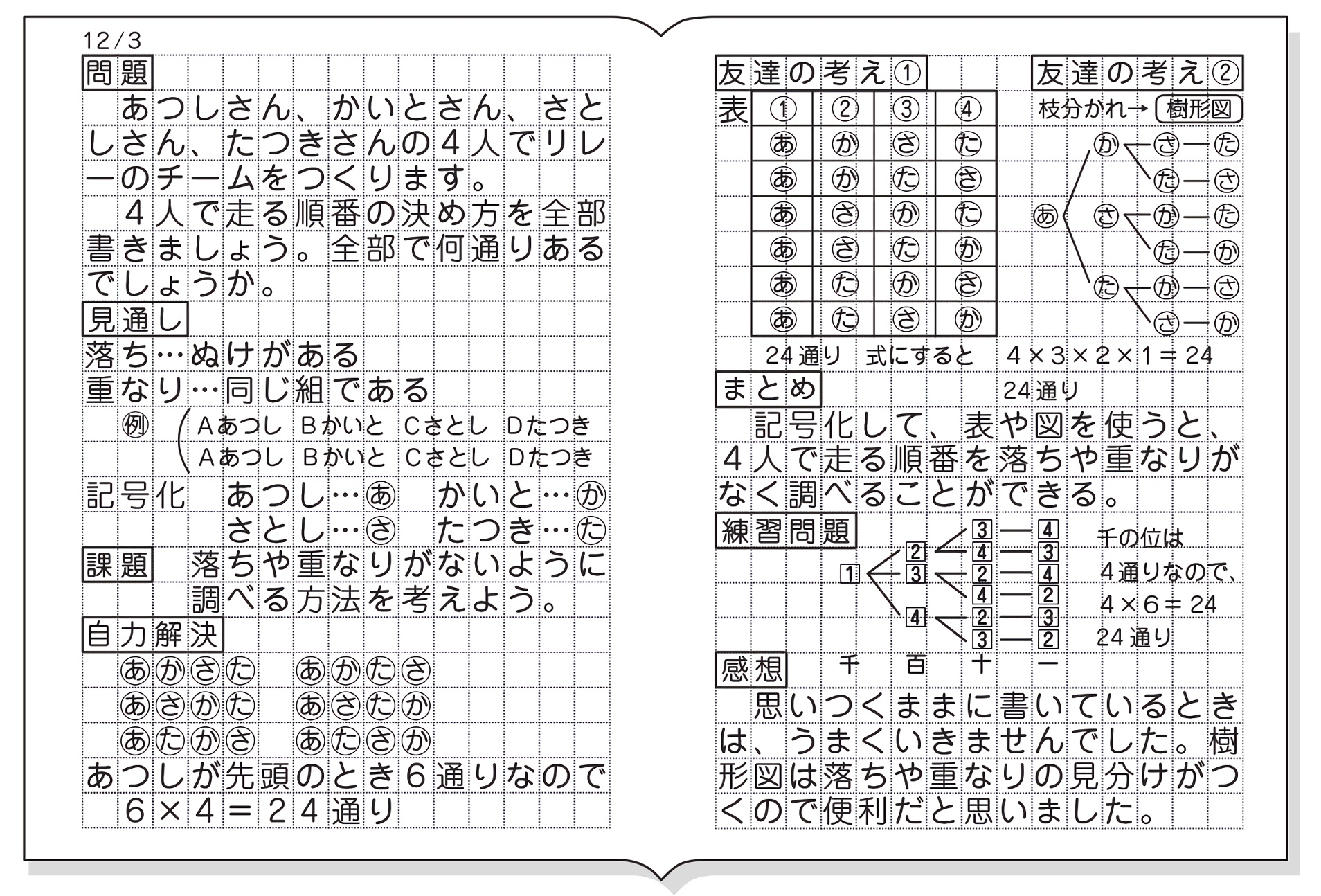



小6算数 場合の数 1 指導アイデア みんなの教育技術




コインの出方は何通り スクールプレゼンター用教材 教材 プリント 学びの場 Com
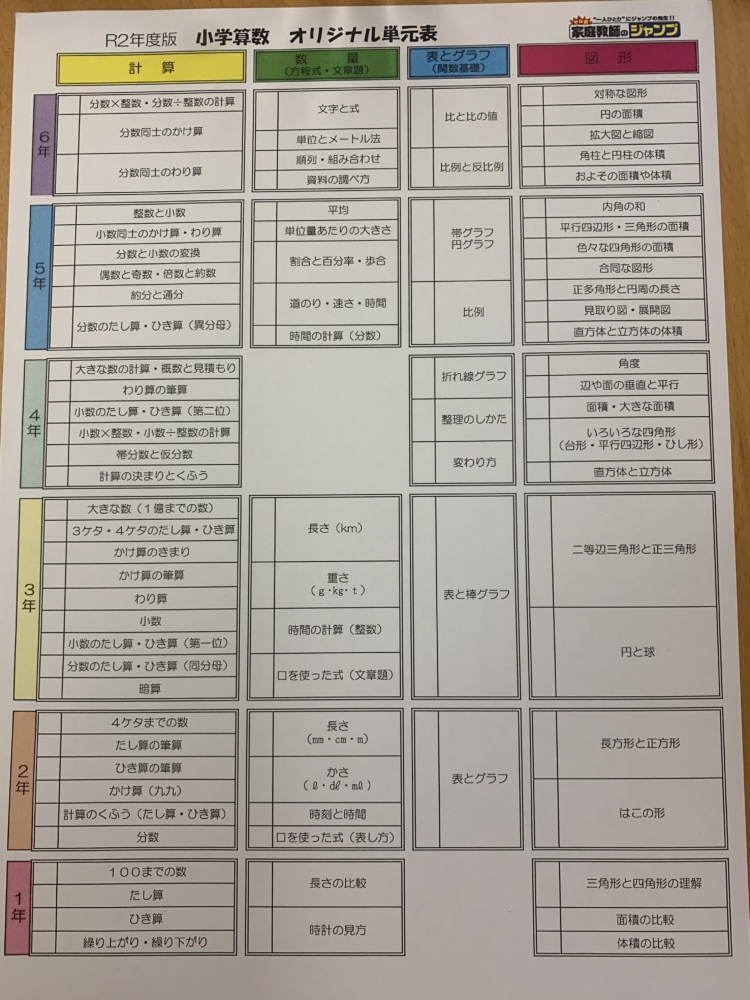



大変 小学生の算数カリキュラム 家庭教師のジャンプ



6年算数場合の数 1 教え方のポイント




リーグ戦とトーナメント戦 小学校6年教材より 身勝手な主張



Http Www Center Ibk Ed Jp Action Common Download Main Upload Id 5878




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



2
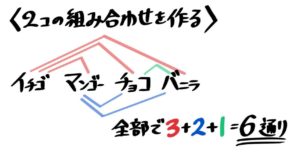



中学受験 場合の数の問題 解き方の総まとめ 数字カード 道順 色分け等 そうちゃ式 受験算数 新1号館 数論 特殊算




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




筑波大学附属小学校算数部



6年生の算数 並べ方と組み合わせ方 立花小学校
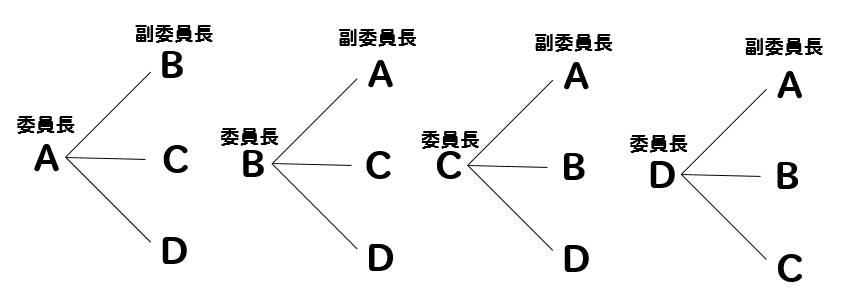



算数 場合の数の解き方は 問題別に考え方を解説 数スタ



Www Pref Kochi Lg Jp Soshiki Files File 1 Pdf




トップ 100 並べ方 と 組み合わせ 方 問題



1




6年生 算数 組み合わせ方は何通り




高校数学 組み合わせ コンビネーション Ncr の計算方法のコツ できるだけ楽に計算しよう 数学の面白いこと 役に立つことをまとめたサイト
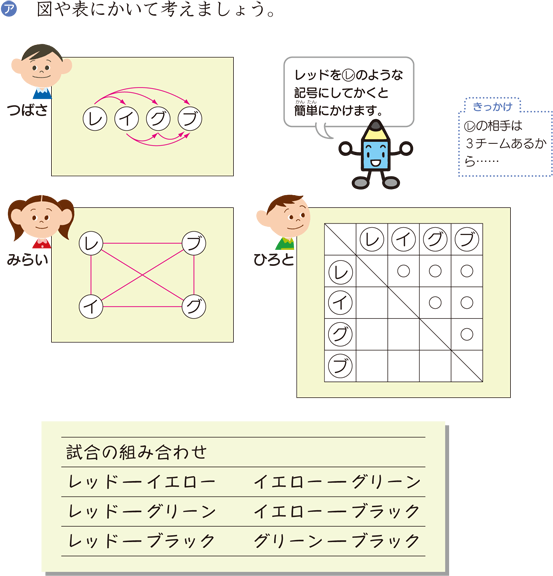



場合の数 算数用語集
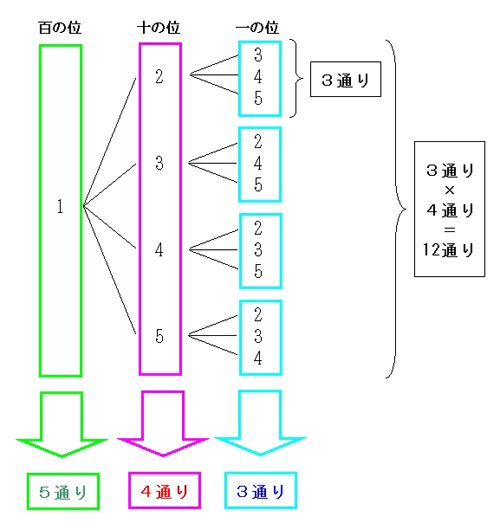



場合の数
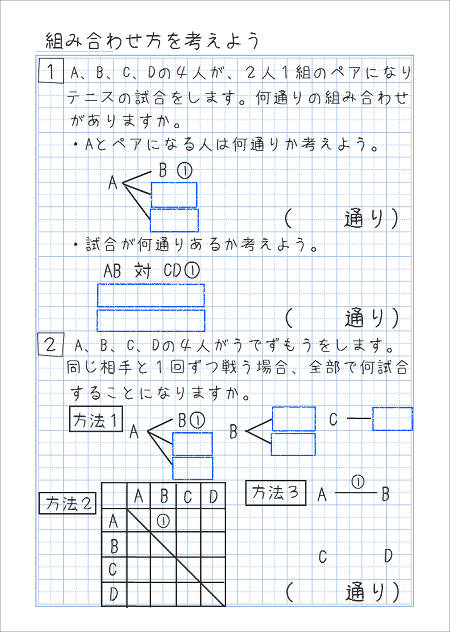



並べ方と組み合わせ方 その1 家庭学習レシピ



6年算数場合の数 1 教え方のポイント



算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素



Www Pref Hiroshima Lg Jp Uploaded Attachment Pdf




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




小学校6年 並べ方と組み合わせ方 並べ方 順列 Youtube




小6算数 場合の数 2 指導アイデア みんなの教育技術
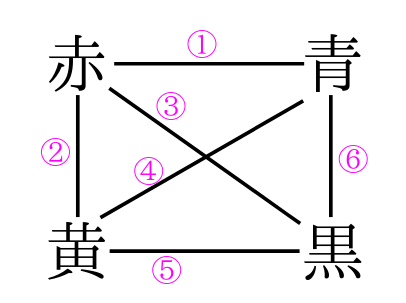



小学校で扱う場合の数の組み合わせの考え方 みけねこ小学校




小6 算数 小6 40 並べ方 組み合わせ方 Youtube




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



小学6年生算数進捗3 最先端家庭学習watch




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




世界一分かりやすい算数 小6 場合を順序よく整理して




250 300 400 450 Descubre Como Resolverlo En Qanda
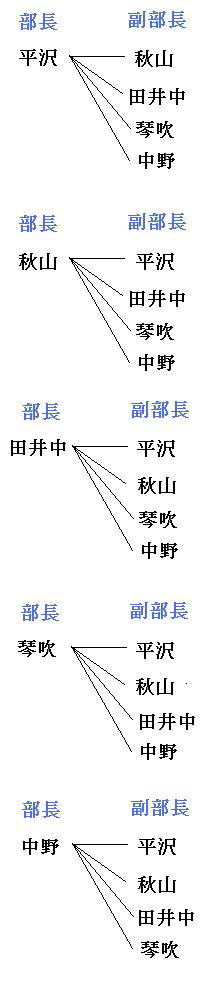



組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける




小6 算数 並べ方と組み合わせ方 小学生 算数のノート Clear
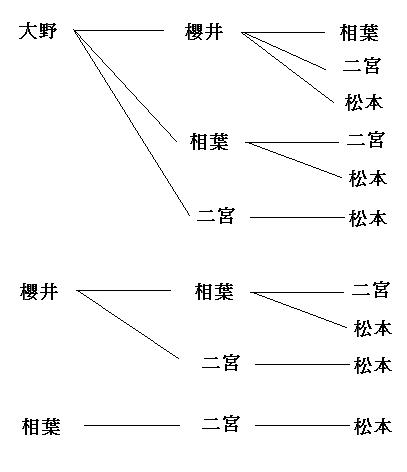



組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける




トップ 100 並べ方 と 組み合わせ 方 問題




小6 算数 小6 39 組み合わせ方 Youtube




トップ 100 並べ方 と 組み合わせ 方 問題
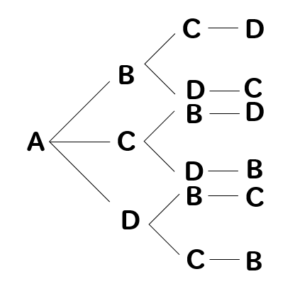



算数 場合の数の解き方は 問題別に考え方を解説 数スタ




算数 場合の数の解き方は 問題別に考え方を解説 数スタ
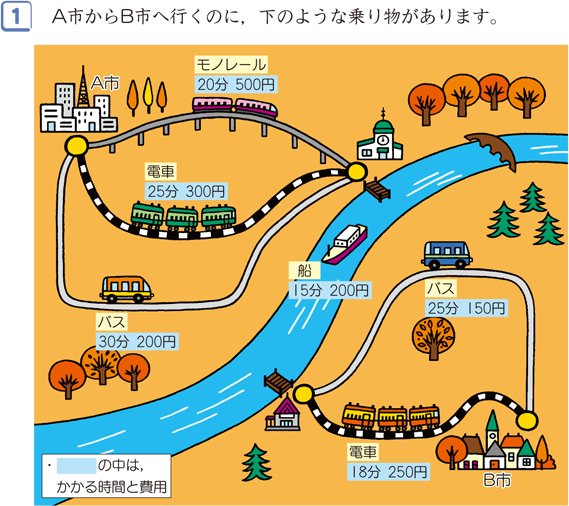



場合の数 算数用語集




スマホok 6年 並べ方と組み合わせ方 場合の数 並べ方を考えよう Youtube
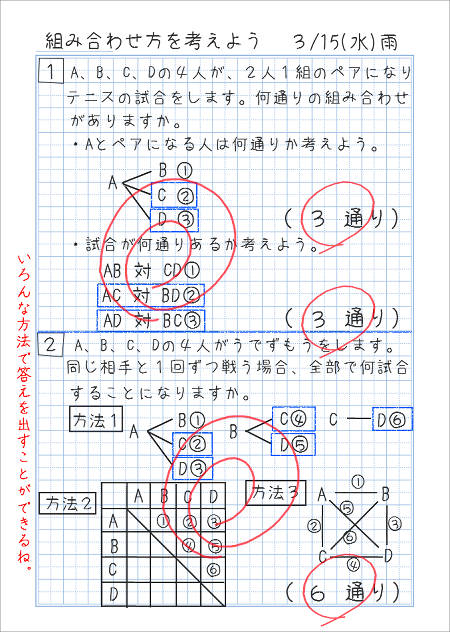



並べ方と組み合わせ方 その1 家庭学習レシピ



増補改訂版 小学校6年分の算数が教えられるほどよくわかる ベレ出版 小学生 算数 分数 教材 小学算数 やりなおし Beret 英語伝 Eigoden 通販 Yahoo ショッピング




小6 算数 並べ方と組み合わせ方 小学生 算数のノート Clear




すきるまドリル 小学6年生 算数 場合の数 無料学習プリント すきるまドリル 無料学習プリント




中野小ブログ 春日部市立中野小学校




6年 算数 組み合わせ



Http Www Kochinet Ed Jp Sukumo E Rokunennkennkyuuzyugyou Pdf
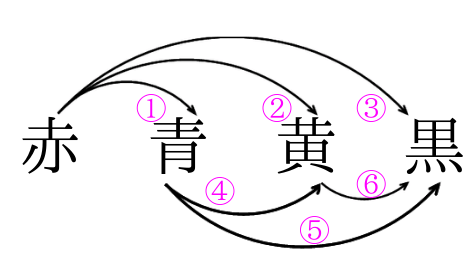



小学校で扱う場合の数の組み合わせの考え方 みけねこ小学校




すきるまドリル 小学6年生 算数 場合の数 無料学習プリント すきるまドリル 無料学習プリント
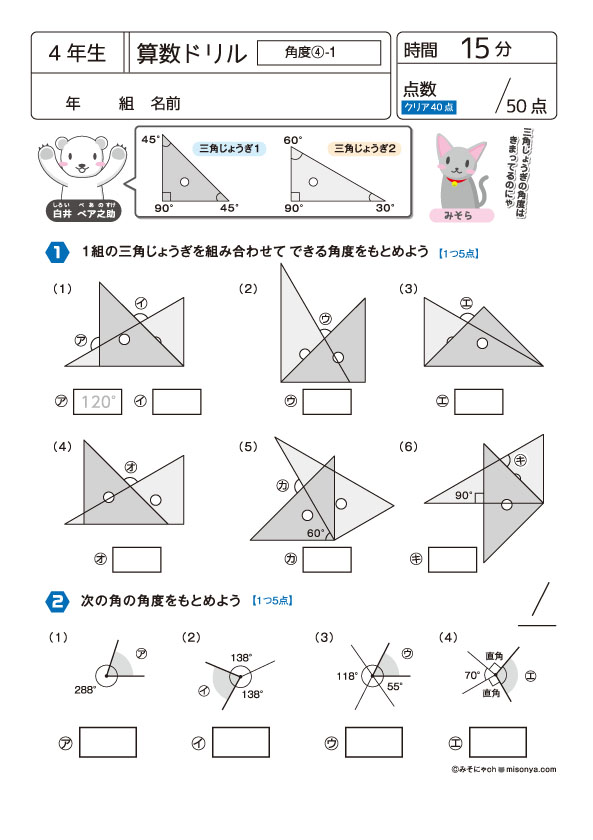



無料の学習プリント 小学4年生の算数ドリル 角度4 総合問題 みそにゃch




場合の数 並べる と 選ぶ の計算方法の違い
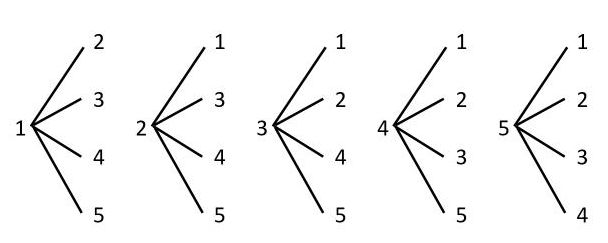



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ




第14講 ならべ方と組み合わせ方 のテスト対策 問題 小6 算数 基礎 スタディサプリ




ケーキの組み合わせ 図や表 スクールプレゼンター用教材 教材 プリント 学びの場 Com



1




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ




Catatan Tentang 並べ方と組み合わせ方 算数 授業ノート Clear




小学6年生の算数 動画 組み合わせ方の問題 19ch




6年算数場合の数 1 教え方のポイント




志布志市立安楽小学校 学校とict sky株式会社 Ictを活用した学習活動をサポート




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




世界一分かりやすい算数 小6 場合を順序よく整理して




小学6年生算数 並べ方と組み合わせ方 単元テストのポイントと攻略法 勉強 英語 教育 子育てに関する相談を承りますーホシバ教育相談所




第26講 並べ方と組み合わせ方 のテスト対策 問題 小6 算数 基礎 入門編 スタディサプリ




小6算数



1




中学受験のための学び方参考書 ここから算数 しっかり基礎力 Amazon Com Books
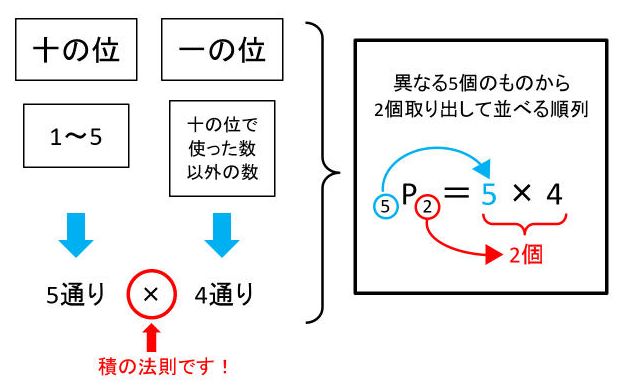



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ



1




場合の数を小学生に教えてみた 一番いい教え方を考えてはみたものの たくべや



2



記事 詳細情報 18年 12月 11日 火曜日 6年生 算数 並べ方と組み合わせ方 a b c dの4チームでバスケットボールの試合をします どのチームも 違ったチームと1回ずつ試合をするとき どんな対戦があるか調べましょう この問題
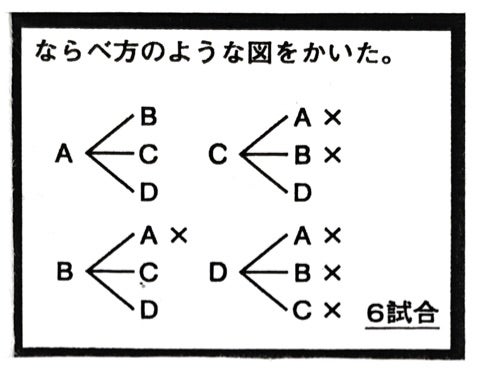



試合の組合せ 算数嫌い0 ゼロ 先生のブログ



Www Pref Hiroshima Lg Jp Uploaded Attachment 1287 Pdf
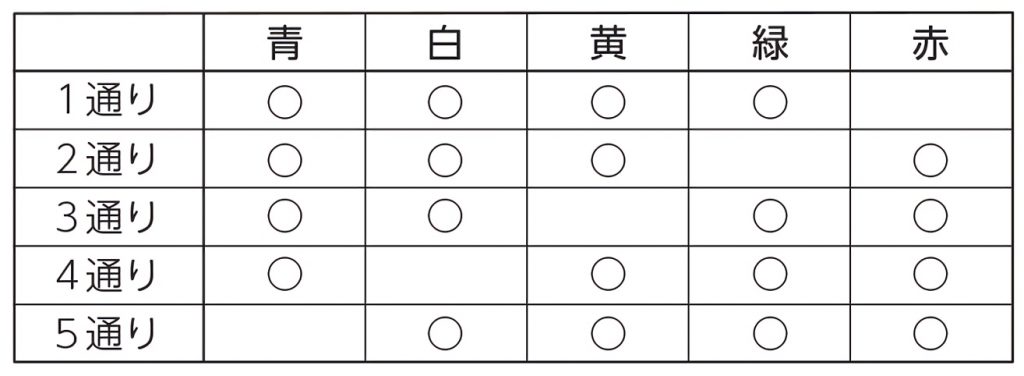



小6算数 場合の数 2 指導アイデア みんなの教育技術




つまずきやすいところが絶対つまずかない 小学校6年間の計算の教え方 安浪 京子 本 通販 Amazon




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




リーグ戦とトーナメント戦 小学校6年教材より 身勝手な主張



0 件のコメント:
コメントを投稿